Covid-19, tests et loi de Bayes
Ou comment ne pas faire confiance à son intuition.
Imaginons qu'une pandémie se déclare et que nous souhaitions tester massivement la population pour rechercher les personnes infectées.
Pour la beauté intellectuelle, supposons qu'une personne sur mille est infectée.
Nous disposons d'un test avec une spécificité de 95%, c'est à dire que 95% des personnes saines testées seront déclarées négatives (et que donc 5% seront déclarées positives à tord).
Votre test est positif, quelle est la probabilité que vous soyez infecté ?
Intuitivement, on est tenté de répondre 95%, vu que le test est fiable à 95%.
En réalité, la probabilité avoisine les 2% !
Cela vous semble totalement aller à l'encontre du bon sens ?
Faisons un peu de maths (ne vous sauvez pas, ils sont simples)
Prenons un groupe de 1000 personnes testées, dans ce groupe nous aurons:
- 1 personne infectée et testée positive. (il y a un malade sur mille)
- 50 personnes saines et testées positives. (5% d'erreurs du test)
- 949 personnes saines et testées négatives. (les autres)
En conséquence, sur les 51 tests positifs, un seul concerne une personne infectée.
En clair, seuls 2% des personnes testées positives sont infectées.
Je comprendrai aisément que certaines personnes trouveront ce résultat difficile à croire, comment accepter qu'un test fiable à 95% se trompe à 98% ?
Cette surprise est un biais cognitif commun appelé "oubli de la fréquence de base".
Notre intuition nous trompe manifestement mais les mathématiques peuvent nous éclairer.
D'un façon plus formelle, posons "+" l'évènement "testé positif", "I" l'évènement "personne infectée" et "S" l'évènement "personne saine"
Alors la loi de Bayes nous dit que:
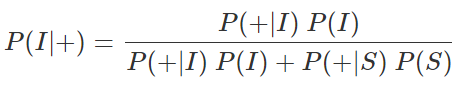
Avec P(+|I)=1, P(I)=0.001, P(+|S)=0.05, P(S)=0.999
Si on fait le calcul, on obtient 1*0.001/(1*0.001+0.05*0.999) = 0.02
Cela confirme notre raisonnement précèdent.
J'ai pris un scenario extrême pour illustrer mon propos avec une faible prévalence (taux d'infection de la population) de la maladie fixée à 1/1000.
Néanmoins, pour une maladie à prévalence faible (rare), on peut affirmer
que pratiquement tous les tests positifs désigneront des personnes saines.
Ce qui ne nous aide pas beaucoup, vous en conviendrez.
D'une façon générale, plus la prévalence de la maladie testée est basse
plus les tests devront êtres précis pour avoir une quelconque valeur.
Intéressons nous maintenant aux tests de la Covid-19.
Introduisons un peu de jargon pour nous faciliter la suite:
- La spécificité (Sp) d'un test est son taux de vrais-négatifs.
- La sensibilité (Se) d'un test est son taux de vrais-positifs.
- La prévalence (P) est le taux de personnes infectées dans la population
- La probabilité d'être infecté avec un test positif, est la Valeur Prédictive Positive
- La probabilité d'être sain avec un test négatif, est la Valeur Prédictive Négative
En appliquant la formule de Bayes, nous obtenons:
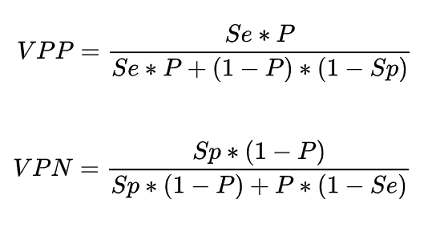
Le test Covid-19 par frottis PCR a une spécificité de 99% et une sensibilité de 70%.
La prévalence de la maladie est aujourd'hui estimée à 20%.
En posant Sp=0.99, Se=0.7 et P=0.2 dans nos formules:
Cela nous donne une Valeur Prédictive Positive de 95%
Cela nous donne une Valeur Prédictive Négative de 93%
En bref, pour un test Covid-19 par frottis PCR
Si le test est positif, il y a 95% de risque que cela soit vrai.
Si le test est négatif, il y a 93% de chance que cela soit vrai.
Vous en conviendrez, la fiabilité de ce test est plus qu'honorable.
Toutefois, vous l'avez compris, quand la pandémie va commencer à refluer, la prévalence va diminuer, ce qui fera aussi diminuer la VPP du test.
Ci dessous le graphique de la VPP et VPN du test en fonction de la prévalence:
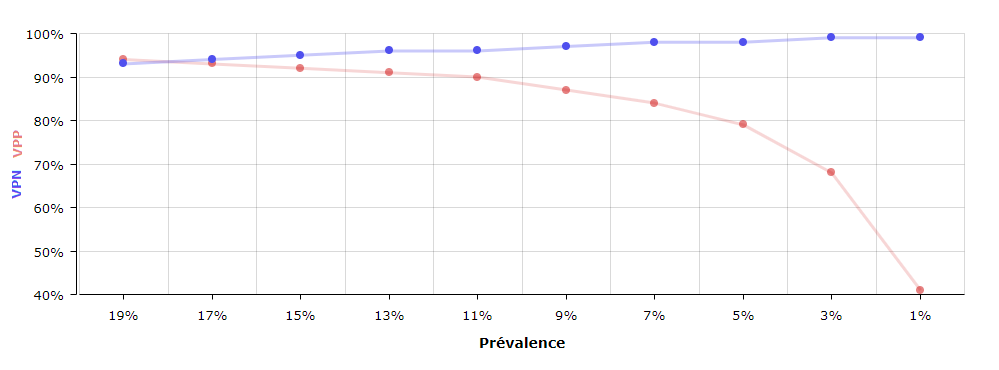
On constate que la VPP décroît très vite à partir d'une prévalence inferieure à 5%.
Quand la prévalence sera de 1% (et on le souhaite tous), la VPP sera de 41%, c'est à dire que plus d'un test positif sur deux sera erroné.
Notons que la VPN ne fera que croitre, ce qui est une bonne chose.
Je vois souvent des articles qui donnent la VPP des tests Covid-19, c'est mathématiquement une erreur car cette dernière dépend de la prévalence qui évolue dans le temps, cela peut conduire à une surévaluation des cas positifs.
En bref, plus la pandémie reculera, plus un test négatif sera significatif et moins un test positif sera significatif.
Espérons que le gouvernement pour décider de nous déconfiner n'utilisera pas le nombre de nouveaux cas dans la population car plus la pandémie reculera, plus les tests donneront des faux-positifs.